티스토리 뷰
계수 정렬(Counting Sort)이란
원소끼리 비교를 하지 않고 원소가 몇번 등장하는지 갯수를 세서 정렬하는 방법이다.
따라서 비교정렬이 아니고 같은 원소의 순서가 바뀌지 않는 안정정렬(stable sort)이다.
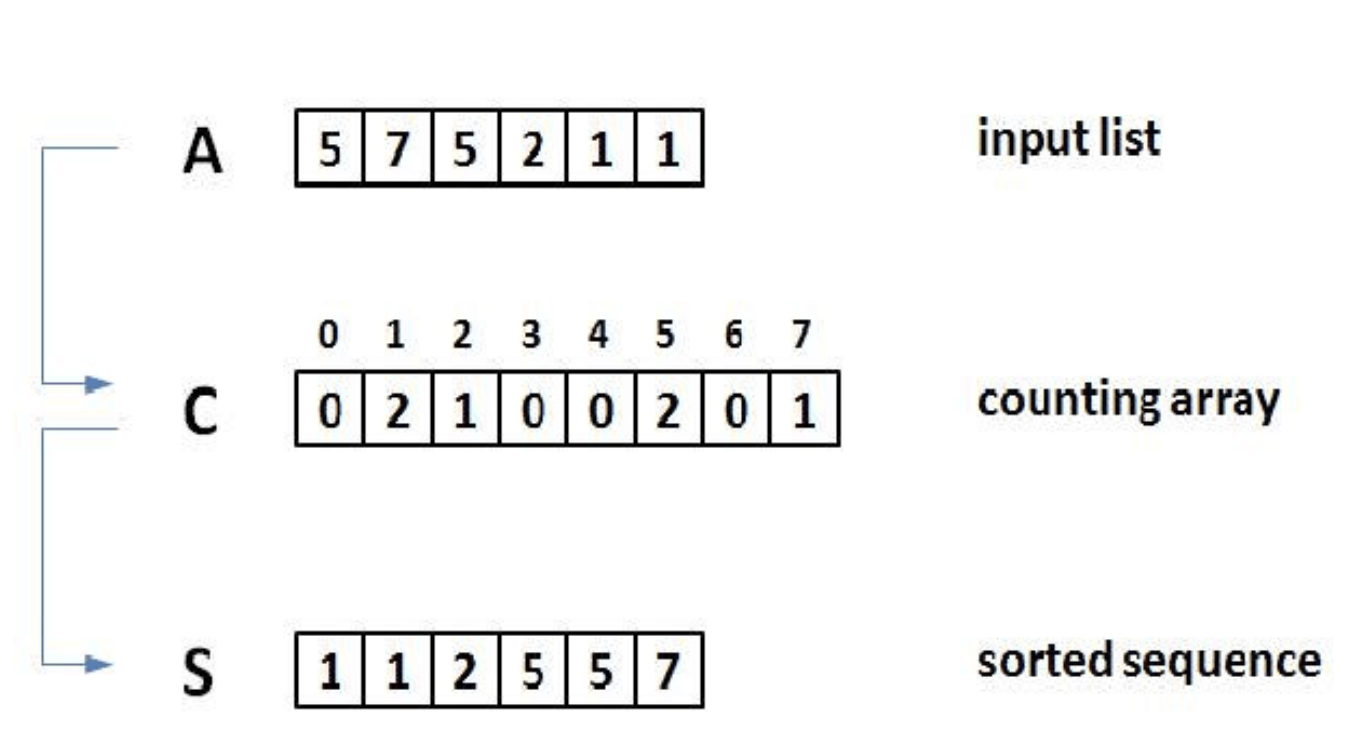
시간복잡도는 O(n + k)으로 퀵정렬, 병합정렬에 비해 일반적으로 빠르다.
k: 정렬할 수들 중 가장 큰 값
n: 정렬할 수의 개수
만약 k가 n보다 작은 수이면 O(n)이 되지만, k가 n보다 매우 큰 수이면 O(무한)이 될 수도 있다.
가장 큰 숫자에 영향을 받는다는 단점이 있다.
만약 정렬해야하는 리스트가 [0, 1, 9999]일때는 배열에 2부터 9998까지 불필요한 공간을 만들어야하기 때문에 비효율적이다.
또, n의 값이 너무 커지면 일반 정렬 알고리즘보다 느려질 수 있으므로 적은 개수의 숫자를 정렬할때 좋다.
정렬할때 숫자 갯수를 저장할 공간(k)과 결과를 저장할 공간(n)이 필요하다. 따라서 O(n+k) 의 공간복잡도를 가진다.
파이썬 코드
# 정렬 전 리스트
before = [3, 4, 0, 1, 2, 4, 2, 4]
# 정렬 후 리스트
after = []
# 빈도를 저장할 공간 (before의 최대값만큼의 크기, 0으로 초기화)
li = [0 for _ in range(max(before)+1)]
# 빈도 세서 저장하기
for each in before:
li[each] += 1
# 빈도수만큼 정렬 후 리스트에 추가
for i in range(len(li)):
num = li[i]
for k in range(num):
after.append(i)
# 정렬 후 리스트 출력
print(after)파이썬의 append()는 O(1)이기때문에 따로 누적합을 구하지 않고 그냥 바로 append해줬다.
정석 알고리즘대로 (누적합을 구하는 방식으로) 짠 코드
# 정렬 전 리스트
before = [3, 4, 0, 1, 2, 4, 2, 4]
# 정렬 후 리스트
after = [-1 for _ in range(len(before))]
# 빈도를 저장할 공간 (before의 최대값만큼의 크기, 0으로 초기화)
li = [0 for _ in range(max(before)+1)]
# 빈도 세서 저장하기
for each in before:
li[each] += 1
# 누적합 구하기
for i in range(len(li)-1):
li[i+1] += li[i]
print(li)
# 누적합을 바탕으로 숫자를 결과에 넣어주기
# 예) 누적합이 [1, 2, 4]인 경우, 0~1에 0, 1~2에 1, 2~4에 3을 넣는것
s = 0
for i in range(len(li)):
for k in range(s, li[i]):
after[k] = i
s = li[i]
# 정렬 후 리스트 출력
print(after)
대표 문제
10989번: 수 정렬하기 3
첫째 줄에 수의 개수 N(1 ≤ N ≤ 10,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 숫자가 주어진다. 이 수는 10,000보다 작거나 같은 자연수이다.
www.acmicpc.net
참고한 포스팅
(Algorithm) 계수 정렬(counting sort)
안녕하세요! 이번 시간에는 계수 정렬에 대해 알아보겠습니다. 계수 정렬은 놀랍게도 작은 숫자에서는 복잡도가 O(n + k)입니다. n+k는 처음 보죠? k가 정렬할 수들 중에 가장 큰 값을 의미하는데요
www.zerocho.com
카운팅 정렬, 래딕스 정렬 · ratsgo's blog
이번 글에서는 요소값을 명시적으로 비교하지 않아도 정렬할 수 있는 기법인 카운팅 정렬(counting sort)과 래딕스 정렬(Radix sort)에 대해 살펴보도록 하겠습니다. 이 글은 고려대 김선욱 교수님 강��
ratsgo.github.io
- Total
- Today
- Yesterday
- 백준
- counting sort
- flutter simultor
- 백준알고리즘
- 코틀린
- 안드로이드
- 프로그래머스
- 시뮬레이터 키보드
- 코틀린 리스트뷰
- kotlin fragment
- 투포인터 알고리즘
- 파이썬 최대공약수
- 안드로이드 키해시
- 코틀린 바텀네비게이션
- 투포인터 알고리즘 파이썬
- 카카오 키해시
- 소수 구하기 파이썬
- 백준 1644
- 카카오톡으로 로그인 오류
- 백준 1806
- 안드로이드 카카오톡으로 로그인
- 카카오 기출
- Kotlin
- 데이터바인딩 뷰바인딩 차이
- 백준 2003
- TextFormField keyboard
- 전화번호목록 파이썬
- 코틀린 뷰바인딩
- 코틀린 뷰페이저
- 코틀린 데이터바인딩
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
